Both the median and quantile calculations in Spark can be performed using the DataFrame API or Spark SQL. You can use built-in functions such as approxQuantile, percentile_approx, sort, and selectExpr to perform these calculations. In this article, we shall discuss how to find a Median and Quantiles using Spark with some examples

Let us create a sample DataFrame with Product sales information and try calculating the Median and Quantiles of Sales using it.

1. Create Sample DataFrame.

Create a sample DataFrame with two columns: “Product” and “Price”. It represents sales information, where each row contains the name of a product and its corresponding price.

//Imports
import org.apache.spark.sql.SparkSession
import org.apache.spark.sql.functions._

// Create a SparkSession
val spark = SparkSession.builder()
.appName(“SalesDataExample”)
.master(“local”)
.getOrCreate()

// Create a sample DataFrame with sales information
val data = Seq(
(“Product A”, 100.0),
(“Product B”, 150.0),
(“Product C”, 200.0),
(“Product D”, 125.0),
(“Product E”, 180.0),
(“Product F”, 300.0),
(“Product G”, 220.0),
(“Product H”, 170.0),
(“Product I”, 240.0),
(“Product J”, 185.0)
)
val df = spark.createDataFrame(data).toDF(“Product”, “Price”)
df.show()

The DataFrame created using the above code looks as below:

//Output
+———+—–+
| Product|Price|
+———+—–+
|Product A|100.0|
|Product B|150.0|
|Product C|200.0|
|Product D|125.0|
|Product E|180.0|
|Product F|300.0|
|Product G|220.0|
|Product H|170.0|
|Product I|240.0|
|Product J|185.0|
+———+—–+

2. Calculating Median in Spark

In Spark, the median is a statistical measure used to find the middle value of a dataset. It represents the value that separates the higher half from the lower half of the data.

Spark provides various statistical functions, including approxQuantile() and median(), which can be used to approximate the median. The approxQuantile function calculates the quantiles of a DataFrame column using a given list of quantile probabilities. By specifying the probability of 0.5, you can approximate the median.

2.1 Using Median function

In Spark calculating the median involves sorting the dataset and finding the middle value. You can sort the DataFrame and extract the middle row(s) to obtain the median value.

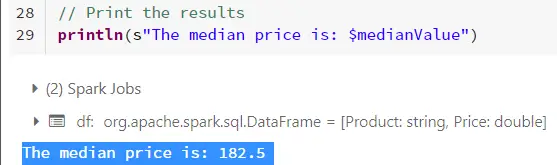
// Calculate the median
val medianValue = df.select(median(col(“Price”))).first().getDouble(0)

// Print the results
println(s”The median price is: $medianValue”)

In this example,

A sample DataFrame is created with two columns: “Product” and “Price”. It represents sales information, where each row contains the name of a product and its corresponding price.

The median function is then applied to the “Price” column of the DataFrame, and the result is a DataFrame with a single row containing the median value.

Finally, the median value is retrieved using the first() function and accessed as a Double using getDouble(0).

The result is printed to the console as

2.2. Using approxQuantile

Spark provides various statistical functions including, approxQuantile which can be used to approximate the median. The approxQuantile function calculates the quantiles of a DataFrame column using a given list of quantile probabilities. By specifying the probability of 0.5, you can approximate the median.

// Calculate quantiles
val quantileProbabilities = Array(0.5)
val quantiles = df.stat.approxQuantile(“Price”, quantileProbabilities, 0.01)

val median = quantiles(0)

// Print the results
println(s”The median price is: $median”)

In the above example,

approxQuantile is called with the column name “prices,” and an array containing the desired quantile probabilities (0.5 in this case for median), and a relative error parameter (0.01 in this example).

The resulting array will contain the approximate quantile values, and you can access them by indexing the array according to the desired percentile.

The resulting median is:

3. Calculating Quantiles in Spark

In Spark, quantiles are statistical measures that divide a dataset into equal-sized intervals. They provide information about the distribution of data and help identify values at specific percentiles. Spark provides a function called approxQuantile that calculates quantiles for a given DataFrame column. This function approximates the quantiles using a set of probabilities and an optional relative error parameter.

Here’s an example of how you can calculate quantiles using approxQuantile in Spark:

// Calculate quantiles
val quantileProbabilities = Array(0.25, 0.5, 0.75)
val quantiles = df.stat.approxQuantile(“Price”, quantileProbabilities, 0.01)

val quantile25th = quantiles(0)
val median = quantiles(1)
val quantile75th = quantiles(2)

// Print the results
println(s”The 25th percentile price is: $quantile25th”)
println(s”The median price is: $median”)
println(s”The 75th percentile price is: $quantile75th”)

In this example,

A sample DataFrame is created with two columns: “Product” and “Price”. It represents sales information, where each row contains the name of a product and its corresponding price.

The approxQuantile is called with the column name “prices,” and an array containing the desired quantile probabilities (0.25, 0.5, 0.75 in this case), and a relative error parameter (0.01 in this example).

The results are printed to the console, including the median price, the prices at the 25th and 75th percentiles. as

Note:

It’s important to note that the approxQuantile function provides an approximation of the quantiles, and the level of approximation can be controlled by adjusting the relative error parameter. If you require precise quantile values, you may need to explore custom approaches or alternative libraries specific to your use case.

4. Conclusion

In conclusion, Spark provides several methods for finding the median and quantiles of a dataset:

Median Calculation:

The approxQuantile function can be used to approximate the median by setting the quantile probability to 0.5. It provides an efficient way to estimate the median value.

Alternatively, sorting the dataset and extracting the middle value(s) can be used to find the exact median.

Quantile Calculation:

The approxQuantile function in Spark allows you to calculate quantiles by specifying the desired quantile probabilities. It provides an approximation of the quantile values.

Overall, Spark’s capabilities for calculating the median and quantiles allow for efficient statistical analysis and insights into distributed computing platforms, making it a powerful tool for processing and analyzing large-scale datasets.

//Imports
import org.apache.spark.sql.SparkSession
import org.apache.spark.sql.functions._

// Create a SparkSession
val spark = SparkSession.builder()
.appName(“SalesDataExample”)
.master(“local”)
.getOrCreate()

val df = spark.createDataFrame(data).toDF(“Product”, “Price”)

// Calculate the median
val medianValue = df.select(median(col(“Price”))).first().getDouble(0)

// Calculate quantiles
val quantileProbabilities = Array(0.25, 0.5, 0.75)
val quantiles = df.stat.approxQuantile(“Price”, quantileProbabilities, 0.01)

val quantile25th = quantiles(0)
val median = quantiles(1)
val quantile75th = quantiles(2)

// Print the results
println(s”The median price is: $medianValue”)
println(s”The 25th percentile price is: $quantile25th”)
println(s”The median price is: $median”)
println(s”The 75th percentile price is: $quantile75th”)

//Result
The median price is: 180.0
The 25th percentile price is: 150.0
The median price is: 180.0
The 75th percentile price is: 220.0

Spark Find Count of NULL, Empty String Values

Spark min() & max() with Examples

Spark map() and mapValues()

Spark RDD vs DataFrame vs Dataset

Spark groupByKey() vs reduceByKey()
Both the median and quantile calculations in Spark can be performed using the DataFrame API or Spark SQL. You can use built-in functions such as approxQuantile, percentile_approx, sort, and selectExpr to perform these calculations. In this article, we shall discuss how to find a Median and Quantiles using Spark with some examples Let us create Read More Apache Spark

Find Median and Quantiles using Spark rimmalapudi Spark By {Examples}