[[{“value”:”
Table of Contents
- Implementing Approximate Nearest Neighbor Search with KD-Trees
- Introduction to Approximate Nearest Neighbor Search
- Construction of KD-Trees
- Querying with KD-Trees
- Step 1: Forward Traversal
- Step 2: Computing the Best Estimate
- Step 3: Backtracking
- Step 4: Termination or Tree Pruning
- Time Complexity of KD-Trees
Implementing Approximate Nearest Neighbor Search with KD-Trees
In this tutorial, you will learn to implement approximate nearest neighbor search using KD-Tree.
Imagine you’re working on a recommendation system for an online retailer, where customers expect personalized suggestions in milliseconds. Or think about a real-time facial recognition system that must match a face in a crowd to a database of thousands. These scenarios demand efficient algorithms to process and retrieve relevant data swiftly.
This is where Approximate Nearest Neighbor (ANN) search algorithms come into play. ANN algorithms are designed to quickly find data points close to a given query point without necessarily being the absolute closest. Recommendation systems on platforms like Netflix and Spotify use ANN to suggest movies and music based on user preferences, ensuring a seamless and personalized experience without the computational burden of exact searches.
One of the most effective methods to perform ANN search is to use KD-Trees (K-Dimensional Trees). KD-Trees are a type of binary search tree that partitions data points into k-dimensional space, allowing for efficient querying of nearest neighbors. This blog post delves into the intricacies of Approximate Nearest Neighbor (ANN) search using KD-Trees, exploring how this data structure can significantly speed up the search process while maintaining a balance between accuracy and computational efficiency.
This lesson is the 1st in a 2-part series on Mastering Approximate Nearest Neighbor Search:
- Implementing Approximate Nearest Neighbor Search with KD-Trees (this tutorial)
- Approximate Nearest Neighbor with Locality Sensitive Hashing (LSH)
To learn how to implement an approximate nearest neighbor search using KD-Tree, just keep reading.
Introduction to Approximate Nearest Neighbor Search
In high-dimensional data, finding the nearest neighbors efficiently is a crucial task for various applications, including recommendation systems, image retrieval, and machine learning.
Imagine a database with billions of samples (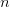 ) (e.g., product specifications, movie metadata, documents, etc.) where comparing all samples with each other produces an infeasible time complexity of
) (e.g., product specifications, movie metadata, documents, etc.) where comparing all samples with each other produces an infeasible time complexity of 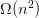 .
.
Traditional exact nearest neighbor search methods (e.g., brute-force search and k-nearest neighbor (kNN)) work by comparing each query against the whole dataset and provide us the best-case complexity of 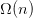 . With
. With 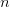 reaching billions, no hardware can process these operations in a definite amount of time.
reaching billions, no hardware can process these operations in a definite amount of time.
As the dataset’s dimensionality and size increase, these exact nearest neighbor search methods become computationally expensive and impractical. So, how can we perform efficient searches in such big databases?
This is where Approximate Nearest Neighbor (ANN) search comes into play, offering a balance between speed and accuracy.
Approximate Nearest Neighbor (ANN) search aims to find points close enough to the true nearest neighbors rather than the exact ones, significantly reducing the computational burden and providing a sub-linear time complexity.
For instance, consider a recommendation system for an online retailer. When a user views a product, the system needs to find similar products from a vast catalog quickly. By using ANN search, the system can efficiently retrieve sufficiently similar products, enhancing the user experience without the need for exhaustive comparisons.
Mathematical Foundation
To understand ANN search, let’s delve into some mathematical concepts. Suppose we have a dataset 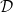 consisting of
consisting of 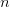 points in
points in 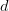 -dimensional space,
-dimensional space, 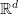 . Given a query point
. Given a query point 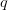 , the goal is to find a point
, the goal is to find a point 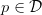 such that the distance
such that the distance 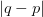 is minimized. In ANN search, we relax this requirement to find a point
is minimized. In ANN search, we relax this requirement to find a point 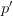 such that:
such that:
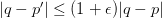
where  is a small positive number representing the allowed approximation error.
is a small positive number representing the allowed approximation error.
KD-Trees for Approximate Nearest Neighbor Search
KD-Trees (K-Dimensional Trees) are a powerful data structure used to organize points in k-dimensional space, making them highly effective for approximate nearest neighbor searches. By partitioning the space into hierarchical regions, KD-Trees allow for efficient querying, significantly reducing the number of distance calculations required. Let’s explore how we can use KD-Trees for Approximate Nearest Neighbor (ANN) search to obtain a balance between speed and accuracy.
Construction of KD-Trees
A KD-Tree (Figure 1) is constructed by recursively splitting the dataset along the median of one dimension at a time, cycling through all dimensions. For example, consider a 2-dimensional dataset of points 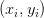 , where
, where 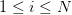 (
(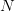 denotes the number of points in the dataset).
denotes the number of points in the dataset).
The first split might be along the x-axis, dividing the points into two halves based on the median x-value. The next split would be along the y-axis, and so on. This process continues until each region contains a small number of points or a single point.
Mathematically, the splitting can be represented as follows:
- Select the dimension
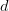 based on the depth of the tree:
based on the depth of the tree: 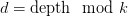
where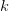 is the number of dimensions.
is the number of dimensions. - Choose the median value
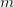 of the points along the chosen dimension
of the points along the chosen dimension 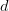 .
. - Partition the points into two subsets:
- Those points with values less than or equal to
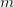 (along dimension
(along dimension 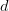 ) go to the left subtree, while
) go to the left subtree, while - Those with values greater than
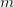 go to the right subtree
go to the right subtree
- Those points with values less than or equal to
Figure 2 shows the final KD-tree after inserting the following 2-dimensional points: (0.53, 0.93), (0.42, 0.64), (0.11, 0.53), (0.27, 0.75), (0.81, 0.61), (0.75, 0.86), (0.64,0.29), (0.61, 0.65), (0.82, 0.75).
With these data points, we construct a KD-Tree (as shown in Figure 2) by first splitting along the x-axis, then the y-axis, and so on.
As shown in Figure 3, the above KD-tree can also be visualized on a cartesian plane where each node split creates new regions.
Querying with KD-Trees
To use KD-Tree for ANN search, we traverse the tree from the root to a leaf node, following the path that is most likely to contain the nearest neighbor. Once a leaf node is reached, we backtrack and explore other branches that could potentially contain closer points, but only if they are within a certain distance threshold.
To understand how querying works, we consider the same KD-tree built in the previous section.
Step 1: Forward Traversal
Now let’s suppose we want to fetch the nearest neighbor for a query 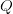 as shown in Figure 4:
as shown in Figure 4:
To find the nearest neighbor to query 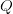 , we start at the root node of the KD-tree. Suppose the root node splits on the x-axis at the median value. We then compare the query point x-coordinate with the median value. If the query point’s x-coordinate is less than the median, move to the left child; otherwise, move to the right child.
, we start at the root node of the KD-tree. Suppose the root node splits on the x-axis at the median value. We then compare the query point x-coordinate with the median value. If the query point’s x-coordinate is less than the median, move to the left child; otherwise, move to the right child.
As shown in Figure 5, we continue this process until we reach a leaf node that corresponds to the region 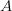 in the plane.
in the plane.
Step 2: Computing the Best Estimate
Now, in that region 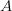 , we find the nearest neighbor to the query
, we find the nearest neighbor to the query 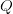
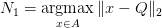
Here, 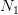 is our best estimate of the nearest neighbor so far (Figure 6).
is our best estimate of the nearest neighbor so far (Figure 6).
Step 3: Backtracking
From Figure 7, we can understand that the current best estimate 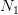 might not be the closest to the query
might not be the closest to the query 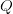 , and there might be points falling in other regions that are closer to
, and there might be points falling in other regions that are closer to 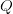 than our current best estimate
than our current best estimate 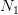 .
.
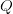 (source: image by the author).
(source: image by the author).To consider such cases, we backtrack to explore other branches that might contain closer points than our current best estimate. The idea is that at each node during backtracking, we calculate the distance from the query point 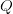 to the splitting hyperplane (Figure 8).
to the splitting hyperplane (Figure 8).
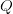 to the splitting hyperplane (source: image by the author).
to the splitting hyperplane (source: image by the author).For instance, if the current node splits on the x-axis at median value 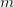 , then the distance from
, then the distance from 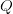 to the hyperplane is:
to the hyperplane is:
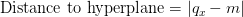
If this distance is less than the distance to the current best estimate 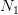 , it indicates that the other branch might contain points closer to
, it indicates that the other branch might contain points closer to 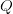 . To this end, we explore the other branch of the subtree, that is, repeat the process from Step 1 to update our current best estimate (Figure 9).
. To this end, we explore the other branch of the subtree, that is, repeat the process from Step 1 to update our current best estimate (Figure 9).
Figure 10 shows the updated best estimate obtained after backtracking.
Step 4: Termination or Tree Pruning
Now, to check whether we want to backtrack again to explore other branches, we will repeat Step 3.
As shown in Figure 11, if the distance of the query point to the nearest splitting hyperplane is greater than its distance to the current best estimate, we prune the other branches and terminate our algorithm.
Time Complexity of KD-Trees
In a brute force approach such as k-Nearest Neighbor, for each query point, the algorithm computes the distance to every point in the dataset to find the nearest neighbor. This results in a time complexity of 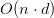 , where
, where 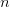 is the number of points in the dataset and
is the number of points in the dataset and 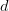 is the dimensionality of the space. This method is straightforward but becomes computationally expensive as
is the dimensionality of the space. This method is straightforward but becomes computationally expensive as 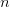 grows.
grows.
KD-Trees, on the other hand, offer a more efficient solution by organizing the data into a binary tree structure. The time complexity for constructing a KD-Tree is 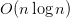 , and the average time complexity for querying the nearest neighbor is
, and the average time complexity for querying the nearest neighbor is 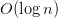 for low-dimensional spaces. However, in high-dimensional spaces, the performance can degrade, approaching
for low-dimensional spaces. However, in high-dimensional spaces, the performance can degrade, approaching 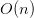 in the worst case due to the curse of dimensionality or, particularly, if the tree is unbalanced or if the search point is far from the root.
in the worst case due to the curse of dimensionality or, particularly, if the tree is unbalanced or if the search point is far from the root.
Implementing KD-Tree for ANN Search
In this section, we will see how KD-trees can help us fetch the nearest neighbors of a query in a quicker way using an approximate nearest neighbor search. We will implement a similar word search functionality that can fetch  similar or relevant words to a given query word. For example, the relevant words to query the word
similar or relevant words to a given query word. For example, the relevant words to query the word "computer" might look like "desktop", "laptop", "keyboard", "device", etc.
We will start by setting up libraries and data preparation.
Setup and Data Preparation
For implementing a similar word search, we will use the gensim library for loading pre-trained word embeddings vector. If you don’t have gensim installed in your environment, you can do so via pip install gensim.
We load the pre-trained GloVe (Global Vectors for Word Representations) model (glove-twitter-25) using Gensim’s API, which provides 25-dimensional word vectors for more than 1 million words. These word vectors are trained from Twitter data making them semantically rich in information.
import gensim.downloader as api
import numpy as np
# Load the pre-trained Word2Vec model
model = api.load("glove-twitter-25")
# Extract all word embeddings into a dictionary
word_embeddings = {word: np.array(model[word]) for word in model.index_to_key}
print(len(word_embeddings.keys()), word_embeddings["computer"].shape)
On Lines 1 and 2, we import the necessary libraries: gensim for loading pre-trained word embeddings and numpy for numerical operations.
On Line 5, we load the pre-trained GloVe model (glove-twitter-25) using Gensim’s API. This model provides us with vector representations of words. On Line 8, we extract all word embeddings from the model into a dictionary called word_embeddings. Each word is mapped to its corresponding vector representation. Finally, on Line 9, we print the number of words in the dictionary and the shape of the embedding for the word "computer".
Setting Up Baseline with the k-NN Algorithm
With our word embeddings ready, let’s implement a k-Nearest Neighbors (k-NN) search. k-NN search identifies the k closest points in a dataset to a given query point by calculating distances (usually Euclidean). It’s useful in classification and regression tasks, finding patterns based on proximity.
However, the k-Nearest Neighbors (k-NN) search algorithm is a brute-force algorithm that finds the nearest points by computing and comparing the distances of a query with all the instances in the corpus. This makes it impractical to use in large-scale applications where the size of search space can be billions (e.g., Google search, YouTube search, etc.).
Let’s see it ourselves by implementing and trying it out for our similar word application.
import time
def knn_search(word_embeddings, query_word, k=5):
# Ensure the query word is in the embeddings dictionary
if query_word not in word_embeddings:
raise ValueError(f"Word '{query_word}' not found in the embeddings dictionary.")
# Get the embedding for the query word
query_embedding = word_embeddings[query_word]
# Calculate the Euclidean distance between the query word and all other words
distances = {}
for word, embedding in word_embeddings.items():
if word != query_word: # Skip the query word itself
distance = np.linalg.norm(query_embedding - embedding)
distances[word] = distance
# Sort the distances and get the top k nearest neighbors
nearest_neighbors = sorted(distances, key=distances.get)[:k]
return nearest_neighbors
t1 = time.time()
nearest_neighbors = knn_search(word_embeddings, 'computer', k=5)
t2 = time.time()
print(f"k-NN search took {t2-t1} seconds")
print("Retrieved neighbors : ", nearest_neighbors)
Output:
k-NN search took 9.19511604309082 seconds Retrieved neighbors : ['camera', 'cell', 'server', 'device', 'wifi']
On Line 10, we import the time module to measure the execution time of the k-NN search.
On Lines 12-30, we define the knn_search function. On Lines 14 and 15, we check if the query word exists in the embeddings dictionary. On Line 18, we retrieve the embedding for the query word. On Lines 21-25, we calculate the Euclidean distance between the query word and all other words, storing these distances in a dictionary. On Line 28, we sort the distances and select the top k nearest neighbors.
Finally, on Lines 32-37, we measure the time taken to perform the k-NN search and print the results. From the output, you can see that it took k-NN search slightly more than 9 seconds to retrieve the 5 similar words to the word 'computer'. This gives us an idea of the performance of our k-NN implementation and sets a baseline for the KD-tree algorithm we will implement now.
Implementing KD-Tree
Now, we will demonstrate how we construct and utilize a KD-Tree for optimized nearest neighbor searches in a set of word embeddings.
from heapq import heappush, heappop
class KDTreeNode:
def __init__(self, split_value, left=None, right=None, axis=0, points=None):
self.split_value = split_value
self.left = left
self.right = right
self.axis = axis
self.points = points
class KDTree:
def __init__(self, word_embeddings, max_samples_per_leaf=100):
# Compute cosine similarity between the target word and all words in the dictionary
self.all_vectors = [(k, v) for k,v in word_embeddings.items()]
self.max_samples_per_leaf = max_samples_per_leaf
self.root = self.build_tree(self.all_vectors)
def build_tree(self, points, depth=0):
if len(points) <= self.max_samples_per_leaf:
return KDTreeNode(
split_value = None,
points=points,
left=None,
right=None,
axis=None
)
k = len(points[0][1]) # Dimension of the points
axis = depth % k
points.sort(key=lambda x: x[1][axis])
median = len(points) // 2
return KDTreeNode(
split_value = points[median][1][axis],
points=points,
left=self.build_tree(points[:median], depth + 1),
right=self.build_tree(points[median + 1:], depth + 1),
axis=axis
)
def k_nearest_neighbors(self, word_vector, k=1):
heap = []
def search(node):
if node.split_value is None: # leaf node
for point in node.points: # get the best estimate in that region
word = point[0]
vec = point[1]
dist = np.linalg.norm(vec - word_vector)
if len(heap) < k:
heappush(heap, (-dist, word))
else:
if -dist > heap[0][0]:
heappop(heap)
heappush(heap, (-dist, word))
else: # non-leaf node
diff = word_vector[node.axis] - node.split_value # compute whether point lies in left or right subtree
close, away = (node.left, node.right) if diff < 0 else (node.right, node.left)
search(close) # search is closest subtree
if len(heap) < k or abs(diff) < -heap[0][0]: # check if distance to splitting hyperplane is less than distance to best estimate so far
search(away)
search(self.root)
return [(word, -dist) for dist, word in sorted(heap, reverse=True)]
# Example usage:
kd_tree = KDTree(word_embeddings, max_samples_per_leaf=5)
On Line 38, we import the heappush and heappop functions from the heapq module, essential for maintaining a heap-based priority queue during our KD-Tree search. The KDTreeNode class is defined on Lines 40-46. This class represents a node in the KD-Tree, storing the split_value, child nodes (left and right), the axis of the split, and the points contained in the node.
Next, on Lines 48-53, we begin defining the KDTree class, which initializes with the word embeddings and a maximum number of samples per leaf node. The embeddings are converted to a list of tuples (self.all_vectors) for easier processing. The build_tree method on Lines 56-79 constructs the KD-Tree recursively. If the number of points is less than or equal to the max_samples_per_leaf, a leaf node is created. Otherwise, points are sorted based on the current axis, and the tree is split at the median, recursively building left and right subtrees.
On Lines 81-104, the k_nearest_neighbors method is responsible for finding the k-nearest neighbors of a given word vector. We use a heap (Line 82) to maintain the closest points found. The nested search function traverses the tree. On Lines 84-94, if a leaf node is reached, we calculate distances for all points in that node and maintain the k closest ones. For non-leaf nodes, on Lines 96-101, we determine which subtree to search based on the query vector’s position relative to the split value and check if the other subtree could contain closer points.
Finally, Line 107 shows how to use the KDTree class. The KD-Tree is instantiated with a maximum of 5 samples per leaf. Finally, we time the search for the nearest neighbors to the word "computer", print the execution time, and retrieve neighbors.
t1 = time.time()
nearest_neighbors = kd_tree.k_nearest_neighbors(word_embeddings["computer"], k=5)
t2 = time.time()
print(f"KD-Tree search took {t2-t1} seconds")
print("Retrieved neighbors : ", nearest_neighbors)
Output:
KD-Tree search took 3.172048568725586 seconds
Retrieved neighbors : [('computer', 0.0), ('camera', 2.2089295), ('cell', 2.3817291), ('server', 2.566226), ('wifi', 2.6789732)]
From the output, we can see that the KD-tree is able to retrieve the same nearest neighbors as k-NN search one-third of the time. This demonstrates the efficiency of the KD-Tree in finding nearest neighbors compared to more straightforward, brute-force methods such as k-NN search.
Note: In practical scenarios, the neighbors retrieved by kd-tree might not be the closest ones. However, by compromising on the precision slightly, one can significantly reduce the computational complexity of the search algorithm.
What’s next? We recommend PyImageSearch University.
86 total classes • 115+ hours of on-demand code walkthrough videos • Last updated: October 2024
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you’re serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you’ll find:
- ✓ 86 courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 86 Certificates of Completion
- ✓ 115+ hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 540+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Summary
This blog post delves into the implementation of Approximate Nearest Neighbor (ANN) Search using KD-Trees. We begin by exploring the significance of ANN Search in various real-world applications, highlighting its ability to balance speed and accuracy in large datasets. The mathematical foundation is laid out, showcasing key distance metrics and their role in finding approximate neighbors efficiently. KD-Trees are introduced as a powerful data structure that partitions data into manageable regions, drastically reducing the computational load compared to brute-force methods.
In the section on KD-Trees for ANN Search, we break down the construction and querying process. Building a KD-Tree involves recursively splitting the dataset along different axes to create balanced partitions. Querying with a KD-Tree is outlined in detailed steps: Forward Traversal to find a leaf node, computing the best estimate, backtracking to check other potential candidates, and termination or tree pruning based on distance metrics. This structured approach ensures efficient retrieval of nearest neighbors.
Time complexity is a crucial consideration, and we analyze how KD-Trees offer significant improvements over traditional methods. The implementation section provides a hands-on guide, starting with data preparation and setting up a baseline with the k-NN algorithm. We then transition to implementing the KD-Tree, showcasing its superior performance in handling large datasets.
By the end of the post, readers will have a comprehensive understanding of KD-Trees and their application in ANN Search. This knowledge equips them with practical insights and code examples, enabling them to implement and optimize KD-Trees in their own projects, thereby enhancing the efficiency of nearest neighbor searches.
Citation Information
Mangla, P. “Implementing Approximate Nearest Neighbor Search with KD-Trees,” PyImageSearch, P. Chugh, S. Huot, G. Kudriavtsev, and P. Thakur, eds., 2024, https://pyimg.co/b7x46
@incollection{Mangla_2024_Implementing-Approximate-Nearest-Neighbor-Search-KD-Trees,
author = {Puneet Mangla},
title = {{Implementing Approximate Nearest Neighbor Search with KD-Trees}},
booktitle = {PyImageSearch},
editor = {Puneet Chugh and Susan Huot and Georgii Kudriavtsev and Piyush Thakur},
year = {2024},
url = {https://pyimg.co/b7x46},
}
To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), simply enter your email address in the form below!

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you’ll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!
The post Implementing Approximate Nearest Neighbor Search with KD-Trees appeared first on PyImageSearch.
“}]] [[{“value”:”Table of Contents Implementing Approximate Nearest Neighbor Search with KD-Trees Introduction to Approximate Nearest Neighbor Search Mathematical Foundation KD-Trees for Approximate Nearest Neighbor Search Construction of KD-Trees Querying with KD-Trees Step 1: Forward Traversal Step 2: Computing the Best Estimate…
The post Implementing Approximate Nearest Neighbor Search with KD-Trees appeared first on PyImageSearch.”}]]  Read More Approximate Nearest Neighbor, KD-Tree, Machine Learning, Nearest Neighbor Algorithm, Tutorial, approximate nearest neighbor, kd-tree, machine learning, nearest neighbor algorithm, tutorial
Read More Approximate Nearest Neighbor, KD-Tree, Machine Learning, Nearest Neighbor Algorithm, Tutorial, approximate nearest neighbor, kd-tree, machine learning, nearest neighbor algorithm, tutorial
