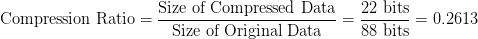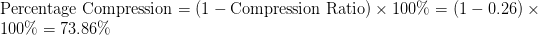[[{“value”:”

Table of Contents

Implementing Huffman Encoding for Lossless Compression

Lossy vs. Lossless Compression

What Is Huffman Encoding?

Summary

Citation Information

Implementing Huffman Encoding for Lossless Compression

In an age where data is continuously growing, and the demand for storage space is ever-increasing, efficient data compression techniques have become crucial. Huffman encoding (named after its inventor, David A. Huffman) is a powerful lossless compression method widely used in various applications.

implementing-huffman-encoding-lossless-compression-featured.png

This algorithm takes advantage of the frequency of occurrence of each data item (e.g., characters in a text) to create variable-length codes, assigning shorter codes to more frequent items and longer codes to less frequent ones. This results in a significant reduction in the overall size of the data without any loss of information, making Huffman encoding an essential tool in the realm of data compression.

Huffman encoding is particularly noted for its simplicity and effectiveness, making it a cornerstone of many compression standards. From reducing the size of text files in ZIP archives to compressing multimedia files like images and audio, this technique has proven indispensable. In this tutorial, we will delve into the intricacies of Huffman encoding, exploring how it works, its advantages, and its various real-world applications.

To learn how to use Huffman encoding for lossless compression, just keep reading.

Lossy vs. Lossless Compression

When it comes to data compression, two primary techniques are used: lossy and lossless compression. Understanding the differences between these methods is essential for choosing the right approach for a given application.

Lossy Compression

Lossy compression techniques (Figure 1) reduce file sizes by permanently eliminating certain information, particularly redundant or less critical data. This results in a significant reduction in file size but at the cost of some loss in quality.

**Figure 1:** Lossy vs. Lossless Compression (source: Imagify).

Common examples of lossy compression include JPEG for images, MP3 for audio, and MPEG for video. These formats are widely used because they achieve high compression ratios, making them ideal for applications where a slight loss in quality is acceptable (e.g., streaming multimedia content over the internet or storing large collections of photos and music).

The main drawback of lossy compression is that once the data is compressed, the discarded information cannot be recovered, potentially affecting the fidelity of the original content.

Mathematically, lossy compression can be represented as:

$hat{x} = f(x)$

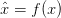
where 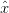$hat{x}$ is the compressed representation, and 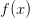$f(x)$ is a function that removes redundancy and less important information from the original data $x$ .

Lossless Compression

In contrast, lossless compression (Figure 1) retains all the original data, ensuring that the decompressed file is identical to the original. Huffman encoding is a prime example of a lossless compression algorithm. By encoding data based on the frequency of occurrence, it achieves compression without any loss of information.

Other common lossless compression methods include Lempel-Ziv-Welch (LZW) used in GIF images and DEFLATE used in ZIP files. Lossless compression is crucial in applications where maintaining the integrity of the data is vital (e.g., text documents, software executables, and scientific data). While lossless methods typically achieve lower compression ratios compared to lossy methods, the benefit is that all original data can be perfectly reconstructed from the compressed file.

Mathematically, lossless compression ensures that:

$x = f^{-1}(f(x))$

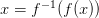
where 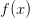$f(x)$ is the compression function and 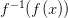$f^{-1}(f(x))$ is the decompression function, meaning the original data $x$ is perfectly recovered.

In summary, the choice between lossy and lossless compression (Figure 1) depends on the specific requirements of the application. Lossy compression is suitable for scenarios where reduced file size is more critical than perfect quality, while lossless compression is essential when data integrity and accuracy cannot be compromised.

What Is Huffman Encoding?

Huffman encoding is a widely used lossless data compression algorithm. David A. Huffman developed it while he was a PhD student at MIT. The Huffman encoding algorithm is known for its efficiency in compressing data without losing any information. The core idea behind Huffman encoding is to use variable-length codes to represent different characters, with shorter codes assigned to more frequently occurring characters and longer codes to less frequent ones. This results in a compressed data representation that is optimal in terms of minimizing the total number of bits used.

The Huffman coding algorithm follows a series of well-defined steps to create the optimal variable-length codes for a given set of data.

Frequency Analysis

First, we analyze the frequency of each character (or symbol) in the input data. This involves counting how many times each character appears in the data (Figure 2). This frequency analysis helps determine which characters occur most and least frequently.

For example, consider the string “ABRACADABRA”:

A: 5 times
B: 2 times
R: 2 times
C: 1 time
D: 1 time

The following code snippet performs the frequency analysis.

from collections import Counter

def frequency_analysis(data):
    frequencies = Counter(data)
    return frequencies

data = "ABRACADABRA"
frequencies = frequency_analysis(data)
print("Frequencies:", frequencies)

Output:

Frequencies: Counter({'A': 5, 'B': 2, 'R': 2, 'C': 1, 'D': 1})

Here, on Line 1, we use the Counter class from the collections module to analyze the frequency of each character in a given string. We define the frequency_analysis function (Lines 3-5), which takes string data as input and returns a Counter object that holds the frequency of each character. By calling frequency_analysis on the string “ABRACADABRA” (Lines 7 and 8), we can count how many times each character appears.

Build a Priority Queue

Next, we create a priority queue (usually implemented as a min-heap) where each node represents a character and its frequency (Figure 3). Nodes with lower frequencies have higher priority (i.e., they are closer to the front of the queue).

**Figure 3:** Building a priority queue (source: image by the author).

The following code snippet creates the priority queue to store the frequency of each character.

import heapq

class Node:
    def __init__(self, char, freq):
        self.char = char
        self.freq = freq
        self.left = None
        self.right = None
        self.isleaf = True

    def __lt__(self, other):
        return self.freq < other.freq

def build_priority_queue(frequencies):
    priority_queue = [Node(char, freq) for char, freq in frequencies.items()]
    heapq.heapify(priority_queue)
    return priority_queue

priority_queue = build_priority_queue(frequencies)
print("Priority Queue:", [(node.char, node.freq) for node in priority_queue])

Output:

Priority Queue: [('D', 1), ('C', 1), ('R', 2), ('A', 5), ('B', 2)]

Here, we first define a Node class ( Lines 12-21) to represent each character and its frequency in the Huffman encoding process. The class has an __init__ method that initializes the character (char), its frequency (freq), pointers to left and right child nodes (left, right), and variable (isleaf) to store whether the node is a leaf node or not.

The __lt__ method (Lines 20 and 21) is defined to enable comparison of Node objects based on their frequencies, which is crucial for building the priority queue using a min-heap. This method ensures that nodes with lower frequencies have higher priority.

The build_priority_queue function (Lines 23-26) takes the character frequencies as input and creates a list of Node objects, each representing a character and its frequency. We use heapq.heapify to convert this list into a priority queue (min-heap), where nodes with the smallest frequencies are given higher priority.

The priority_queue variable holds this priority queue, and the print statement at the end displays the characters and their frequencies in the priority queue (Lines 28 and 29).

Construct the Huffman Tree

To build the Huffman tree, we repeatedly combine the two nodes with the lowest frequencies from the priority queue to form a new node. This new node has a frequency equal to the sum of the two combined nodes. We then insert this new node back into the priority queue (Figure 4).

**Figure 4:** Constructing the Huffman tree: Iterations 1 and 2 (source: image by the author).

We continue this process until there is only one node left, which becomes the root of the Huffman tree (Figure 5).

**Figure 5:** Constructing the Huffman tree: Iterations 3 and 4 (source: image by the author).

The following code snippet creates the Huffman tree, as explained above.

def build_huffman_tree(priority_queue):
    while len(priority_queue) > 1:
        left = heapq.heappop(priority_queue)
        right = heapq.heappop(priority_queue)
        merged = Node(left.char + right.char, left.freq + right.freq)
        merged.left = left
        merged.right = right
        merged.isleaf = False
        heapq.heappush(priority_queue, merged)
        print("Priority Queue:", [(node.char, node.freq) for node in priority_queue])
    return heapq.heappop(priority_queue)

huffman_tree = build_huffman_tree(priority_queue)
print("Huffman Tree Root Frequency:", (huffman_tree.char, huffman_tree.freq))

Output:

Priority Queue: [('R', 2), ('B', 2), ('A', 5), ('DC', 2)]
Priority Queue: [('DC', 2), ('A', 5), ('RB', 4)]
Priority Queue: [('A', 5), ('DCRB', 6)]
Priority Queue: [('ADCRB', 11)]
Huffman Tree Root Frequency: ('ADCRB', 11)

On Lines 30-40, we define the build_huffman_tree function, which constructs the Huffman tree from the priority queue. The function repeatedly removes the two nodes with the lowest frequencies using heapq.heappop (Lines 31-33) and merges them into a new node with a combined frequency (Line 34).

This new node becomes a parent of the two nodes, with left and right pointing to the original nodes (Lines 35-37). The merged node is then pushed back into the priority queue using heapq.heappush (Line 38). This process continues until only one node remains in the priority queue, which becomes the root of the Huffman tree. The final line prints the frequency of the root node, indicating the total frequency of all characters combined (Lines 42 and 43).

Generate Huffman Code

With the Huffman tree constructed, we generate the Huffman codes by traversing the tree from the root to each leaf node. Assign a 0 for left branches and a 1 for right branches. The code for each character is formed by concatenating these bits along the path from the root to the character’s leaf node (Figure 6).

For example, let’s traverse the tree:

A: 0
B: 111
C: 101
D: 100
R: 110

**Figure 6:** Generating Huffman codes (source: image by the author).

The following code snippet generates the Huffman code of all characters in the string, as explained above.

def generate_huffman_codes(node, current_code="", codes={}):
    if node is None:
        return
    if node.isleaf:
        codes[node.char] = current_code
    generate_huffman_codes(node.left, current_code + "0", codes)
    generate_huffman_codes(node.right, current_code + "1", codes)
    return codes

huffman_codes = generate_huffman_codes(huffman_tree)
print("Huffman Codes:", huffman_codes)

Output:

Huffman Codes: {'A': '0', 'D': '100', 'C': '101', 'R': '110', 'B': '111'}

The generate_huffman_codes function (Lines 44-51) recursively traverses the Huffman tree to assign binary codes to each character. Starting from the root node, it appends "0" for left branches and "1" for right branches to form the binary code (Lines 49 and 50). If the node is a leaf node, it stores the current code in the codes dictionary corresponding to the character in the node. The final dictionary, huffman_codes, holds the binary code for each character, which is printed at the end (Lines 53 and 54).

Encode the Data

Finally, replace each character in the input data with its corresponding Huffman code (Figure 7). Using our example string “ABRACADABRA”:

“ABRACADABRA” → “01111100101010001111100”

**Figure 7:** Encoding the data using Huffman codes (source: image by the author).

The string “ABRACADABRA” consists of 11 characters. Assuming each character is encoded using a fixed 8-bit ASCII code, the total size of the original data is:

$11 text{ characters } times 8 text{ bits/character } = 88 text{ bits}$

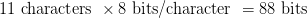
The compressed representation “01111100101010001111100” consists of 23 bits.

The compression ratio is calculated as the size of the compressed data divided by the size of the original data:

$text{Compression Ratio} = displaystylefrac{text{Size of Compressed Data}}{text{Size of Original Data}} = displaystylefrac{22 text{ bits}}{88 text{ bits}} = 0.2613$

$text{Percentage Compression} = (1 - text{Compression Ratio}) times 100% = (1 - 0.26) times 100% = 73.86%$

So, the data compression achieved in this example is 75%, meaning the compressed data is 75% smaller than the original data. This demonstrates the efficiency of Huffman encoding in reducing the size of data without losing any information.

Here’s the code snippet for the same.

def encode_data(data, huffman_codes):
    encoded_data = ''.join(huffman_codes[char] for char in data)
    return encoded_data

encoded_data = encode_data(data, huffman_codes)
print("Encoded Data:", encoded_data)

original_size = len(data) * 8
compressed_size = len(encoded_data)

compression_ratio = compressed_size / original_size
percentage_compression = (1 - compression_ratio) * 100

print("Original Size (bits):", original_size)
print("Compressed Size (bits):", compressed_size)
print("Compression Ratio:", compression_ratio)
print("Percentage Compression:", percentage_compression)

Output:

Encoded Data: 01111100101010001111100
Original Size (bits): 88
Compressed Size (bits): 23
Compression Ratio: 0.26136363636363635
Percentage Compression: 73.86363636363636

The encode_data function converts the original data into its encoded binary form using the Huffman codes, effectively compressing the data (Lines 55-60). By replacing each character with its corresponding Huffman code, the function returns the compressed data.

The subsequent lines (Lines 62-71) calculate the original and compressed data sizes, the compression ratio, and the percentage compression. This allows us to quantify how much data compression Huffman encoding achieves.

Decode the Data

Once we have our encoded data and the Huffman tree, decoding the data back to its original form is straightforward. The process involves traversing the Huffman tree based on the binary codes in the encoded data to reconstruct the original characters. Here’s how we do it:

Initialize: Start at the root of the Huffman tree. Read each bit from the encoded data one by one.
Traverse the Tree: If the bit is 0, move to the left child node; if the bit is 1, move to the right child node.
Reach a Leaf Node: When we reach a leaf node (a node with a character), we decode that character and append it to our decoded data.
Repeat: Reset to the root of the tree and continue reading the next bits of the encoded data until all bits are processed.

Here’s the code to implement this:

def decode_data(encoded_data, huffman_tree):
    decoded_data = []
    current_node = huffman_tree
    for bit in encoded_data:
        if bit == '0':
            current_node = current_node.left
        else:
            current_node = current_node.right
        if current_node.isleaf:
            decoded_data.append(current_node.char)
            current_node = huffman_tree
    return ''.join(decoded_data)

decoded_data = decode_data(encoded_data, huffman_tree)
print("Decoded Data:", decoded_data)

Output:

Decoded Data: ABRACADABRA

This function decode_data (Lines 72-83) takes the encoded data and the Huffman tree as inputs. It traverses the tree according to the bits in the encoded data, appending each decoded character to the decoded_data list. Finally, it joins the list into a single string, which is the reconstructed original data. This process ensures that we can accurately recover the original data from the compressed binary format (Lines 85-86).

What’s next? We recommend PyImageSearch University.

Course information:
86 total classes • 115+ hours of on-demand code walkthrough videos • Last updated: October 2024
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled

I strongly believe that if you had the right teacher you could master computer vision and deep learning.

Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?

That’s not the case.

All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.

If you’re serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.

Inside PyImageSearch University you’ll find:

&check; 86 courses on essential computer vision, deep learning, and OpenCV topics
&check; 86 Certificates of Completion
&check; 115+ hours of on-demand video
&check; Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
&check; Pre-configured Jupyter Notebooks in Google Colab
&check; Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
&check; Access to centralized code repos for all 540+ tutorials on PyImageSearch
&check; Easy one-click downloads for code, datasets, pre-trained models, etc.
&check; Access on mobile, laptop, desktop, etc.

Click here to join PyImageSearch University

Summary

In this tutorial, Implementing Huffman Encoding for Lossless Compression, we dive into the world of data compression, explaining the key differences between lossy and lossless compression techniques. We discuss how lossy compression, though efficient, results in some loss of data, making it suitable for applications where a slight reduction in quality is acceptable. On the other hand, lossless compression retains all original data, ensuring perfect reconstruction, which is crucial for applications requiring data integrity.

We then introduce Huffman encoding, a powerful lossless compression technique that optimizes data representation by assigning shorter codes to more frequent characters. We walk through the steps of the Huffman encoding process, starting with frequency analysis to determine the occurrence of each character in the data. Next, we build a priority queue to efficiently manage these frequencies and construct the Huffman tree, a binary tree structure that helps generate the optimal variable-length codes.

Finally, we guide you through the encoding and decoding processes. We show how to replace each character in the original data with its corresponding Huffman code to compress the data, and we provide a method for decoding the compressed data back to its original form using the Huffman tree. By the end of the post, we illustrate how Huffman encoding achieves significant data compression without losing any information, making it an essential tool in various applications requiring efficient data storage and transmission.

Citation Information

Mangla, P. “Implementing Huffman Encoding for Lossless Compression,” PyImageSearch, P. Chugh, S. Huot, and P. Thakur, eds., 2025, https://pyimg.co/t2swr

@incollection{Mangla_2025_implementing-huffman-encoding-lossless-compression,
  author = {Puneet Mangla},
  title = {{Implementing Huffman Encoding for Lossless Compression}},
  booktitle = {PyImageSearch},
  editor = {Puneet Chugh and Susan Huot and Piyush Thakur},
  year = {2025},
  url = {https://pyimg.co/t2swr},
}

To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), simply enter your email address in the form below!

Download the Source Code and FREE 17-page Resource Guide

Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you’ll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!

The post Implementing Huffman Encoding for Lossless Compression appeared first on PyImageSearch.

“}]] [[{“value”:”Table of Contents Implementing Huffman Encoding for Lossless Compression Lossy vs. Lossless Compression Lossy Compression Lossless Compression What Is Huffman Encoding? Frequency Analysis Build a Priority Queue Construct the Huffman Tree Generate Huffman Code Encode the Data Decode the Data…
The post Implementing Huffman Encoding for Lossless Compression appeared first on PyImageSearch.”}]] Read More Huffman Coding, Huffman Encoding, Huffman Tree, Lossless Compression, Tutorial, huffman code, huffman coding, huffman encoding, huffman tree, lossless compression, lossy vs lossless, tutorial

Implementing Huffman Encoding for Lossless Compression Puneet Mangla PyImageSearch

Implementing Huffman Encoding for Lossless Compression

Lossy vs. Lossless Compression

Lossy Compression

Lossless Compression

What Is Huffman Encoding?

Frequency Analysis

Build a Priority Queue

Construct the Huffman Tree

Generate Huffman Code

Encode the Data

Decode the Data

What’s next? We recommend PyImageSearch University.

Summary

Citation Information

Download the Source Code and FREE 17-page Resource Guide

Leave a Reply Cancel reply